基礎の前の話
ディープランニングについて調べたので、自分自身の再学習の為に
中学生にも理解できそうな感じで説明してみる
厳密には、事実と異なる記載も・・・?
その辺は目をつぶろうね、なんとなくお伝えするためだ
今更な感じは、ありますけどね・・・
ディープランニングとは?
機械学習の一部分で、
機械学習とは、AI(人工知能)の一部分の内容です
AI > 機械学習 > ディープランニング
こんな感じかな・・・
AI(人工知能)って何だ?と言われると・・・
『人間のように考える機械のこと』と答えることになる
『はぁ?』
と思う人もいますかね?
そもそも論として、AI(人工知能)って何に使う?
何で必要なの?
そんなもの・・・
個人的な考えを言うと
貴方も、楽しい事(娯楽・遊び)って好きでしょ?
楽したい、サボりたいでしょ?
企業・会社の社長って、お金を儲けたいよね?
会社が儲かると、従業員に沢山の給料を払える
貴方や、貴方の家族(父・母とか)に、お金が回って来るわけだ
AI(人工知能)って、金儲けや娯楽とかに役立つんだ
AI(人工知能)
それは既に、至る所に存在している
例えば
貴方が突然、オセロゲームをやりたくなった
しかし、対戦相手がいない
そこで、オセロゲームのソフトで、CPU対戦で遊ぶ
他にも将棋や囲碁、ポーカーとか
CPU対戦・・・
そうです、これAIです。
家庭用ゲーム機やスマホのゲーム、ゲームセンターのゲーム機って・・・
敵キャラ出てくるよね?
これAI
自動車の自動運転技術・・・これもAI
身近なところだと、天気予報もAIをつかう
そういえば、エアコンも使ってるよね?AI
企業は、売上予測、在庫管理とかにもAI
ネットの広告表示、あなたにおススメ商品もAI使っている
普段気にしないだけでAIは、既に生活の一部なんだ
調べれば、そこら中に使われている
AIって、物凄く沢山の種類があって、その中の1つにディープランニングがある
ディープランニングは、何が凄いの?
AIは、我々の生活を豊かにしてくれる技術なんだが
数あるAIの技術の中で、ディープランニングは注目されている
ディープランニングは、壁をブチ破った!!技術なんだ
ある分野で、プロ・人間を凌駕する結果を残した
今まで人間にしかできない分野
高度な思考、経験が必要な判断を、機械が出来るようになったんだよ!
しかし・・・
人間を凌駕する技術って、それほど珍しくない
例えば
自転車、バイク、自動車、電車、飛行機は、人間より速いだろ?
例えば
油圧ジャッキ、フォークリフト、クレーン、人間の力で動かせる荷物より
何倍も重い荷物を、動かせるだろ?
それでも凄い、ディープランニング
今までできなかった、新たな分野を切り開いた
ここが凄いところ!
一部分ではあるが、分類、判断の分野で、機械化ができるようになったんだ
分類、判断の機械化が進む
分類、判断は人間以外にはできなかった(難易度が滅茶苦茶)
それが機械ができるようになる
人間って24時間、365日不眠不休で、働くことは不可能だ
死んでしまう
でも、機械なら可能だ
人間て、能力に差があるだろ?
汚い言葉になるが
馬鹿な人間、仕事ができない人間もいる
でも、機械の能力は保証されている
人間には、最低賃金があるが、機械にはない
コストが安いんだ
賃金安くて、24時間働き、文句も言わない
判断力も専門家を打ち負かす!
企業や会社の社長は、何処かAIに任せられないか?
AIで、今までにない商品を作れないか?
駄目な社員を解雇して、入れ替えたい
と大注目なわけだ
ディープランニングの前に・・・
他のAI技術はどうだろう?
例えば
赤リンゴと青リンゴを画像を判断するAIを作る場合
まずリンゴの画像データ(赤と青とその他はずれ)を用意する
何を根拠に判断するかを、人間がその特徴考え、
その方法を人間が、事細かに機械に教える必要がある
AIの何とかという技術を使って、これとこれを組み合わせるんだ!
といった感じで
データを使って何度も人間が試行錯誤し、
使うAI技術や特徴を変えながら何度も何度もテストをして完成となる
大体こんな感じだ
ではディープランニングは?
ディープランニングの面白いところは、データを用意するだけでいいところだ
ディープランニングという、既に完成された汎用AIがあって
この汎用AIに
これは赤リンゴだよ
これは青リンゴだよ
と画像データをたくさん与えると
その後は、全自動で!
何度も何度も繰り返し学習し、判断ができるようになるわけ
人間が特徴を教えたり、試行錯誤する必要がない
勉強の終えたAIに対して画像を放り込むと

青リンゴ!

赤リンゴ!

はぁ?
と返事が返ってくる・・・
とイメージすればよい
こんなの分類しても役に立たないと思うかもしれないが・・・
胸のレントゲン画像だと、どうだろうか?
新米医師もいる、勉強熱心な医師もいる、ヤブ医者だっている
レントゲン画像を、放り込むだけで
肺炎!、喘息!、骨が折れてる!、心臓に異常あり!
という回答が高精度で得られる
そんなことが近い将来可能になるかもしれない
凄い技術だろ?
これを現実にするには、たくさんのデータとディープランニングに精通した
すぐれた技術者がたくさん必要になるんだけど
ディープランニングに興味は出たかな?
次は仕組みだ!
ディープランニングの仕組み?
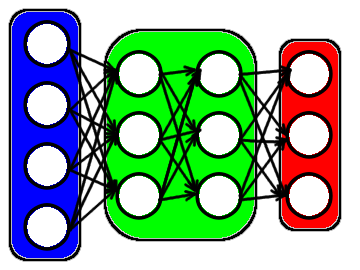
ディープランニングと言えば、上のような図がよく出てくる
自分で書いたので汚い図で申し訳ない、略図だ
人間の神経を機械上再現する仕組みになる
青が入力層、緑が隠れ層、赤が出力層だ
丸が1つの人工ニューロンで、種類は色々ある
パーセプトロン、シグモイドニューロンとか様々だ
この構造が、ディープラーニング(深層学習)の仕組みとなる
深層学習・・・
そう、深層で、学習なのだ
学習は、勉強のことで、深層は、層が深いんだ
深くなるのは、緑の部分、隠れ層と呼ばれる部分が深くなる
略図では、丸が3つ並び、2列となっているが・・・
大規模なものでは、列数も千を超え、1列の丸(ニューロン)も
1万を超えたりする
それが、網目状に繋がっていく
だから日本語では、深層の学習、深層学習と呼ばれる
たぶんな・・・ 知らんけど
この丸は、何をするのだろうか?
別の丸から数字を貰い、別の丸に数字を届ける
0個・4個・100個・1000個・・・沢山の丸と繋がり数字を貰い
これまた、1個から沢山の丸へと数字を渡す
貰う数字は、様々だが、渡す数字は1つのみ
これを沢山の丸に配ることになる
受け渡す数字だが、シンプルだと0~1の範囲
0とか1とか0.5とか0.837663232455とかを、やり取する
はぁ?
って感じだろ?
なんでこんなので、赤リンゴと青リンゴを区別できんの?
自分は初め不思議に思ったが、勉強すると仕組みが理解できる
数式を導くのは、無理だったがな・・・
丸(ニューロン)って、数字を貰って、数字を出すだろ?
リンゴの画像は、数字じゃない
という事は、学習できないじゃんか?
と思わないか?
えっ・・・
思わないって・・・
天才は、馬に蹴られてしまえ!
画像を数字へと変える前処理が、必要になる
リンゴの画像を、0~1の範囲へと変換するんだ
前処理が必要だ
画像って点で、出来てるって知っているかな?

こんな感じで・・・ ↑
テレビとか、PCモニター、スマホの画面を虫眼鏡で拡大するとわかるよ
一つの点は、R・G・Bの数字で保存されている・・・たぶん
一般的なのは256段階で、0~255・・・ のはずだが?何か問題でも?
点の数字を各成分(RGB)毎に、すべて255で割ってやる
すると
0÷255 = 0
255÷255 =1
128÷255 = 0.5019607843137255
となり、 0~1 の範囲に収まる
1つの画素から3つの数字ができるから、3つのニューロンにそれぞれ入力する
これをすべての点で、やらなくてはいけない
入力層の別々のニューロンへと入れるわけだ
別々だ!
同じニューロンに別の画素のデータを入れたらだめだぞ
ちなみにだが、画像の大きさはすべて同じにする必要がある・・・たぶん
学習は各画像の同じ位置にある情報を、同じニューロンに入れることで
各画像の同じ位置の点情報、この違いを学習するわけだ
その結果、出力層のニューロンが、0~1の数字を吐き出す
一番上のニューロン、真ん中、一番下が、それぞれ別の数字を出すはずだ
学習とは、ある種類の画像を入力したとき、特定の数字を出すように、
隠れ層のニューロンを調整することだ
リンゴの分類では、
赤リンゴの時に、1番目は1、真ん中は0、一番下は0
青リンゴの時に、1番目は0、真ん中は1、一番下は0
素敵な人の時に、1番目は0、真ん中は0、一番下は1
が出るように、といった感じだ
実際は1とか0は出ることは、まず無くて
0.976とか、0.012とか、ほぼ1とか、ほぼ0が出力される
学習が不十分とか、ニューロンの数が少ないとか、
層が薄い、データが少ない、データが悪いと
0.5126562781とか0.4928177とか出てきて
判別不能な場合もある
出力層のニューロンが、それぞれ吐き出す数字から、分類を判断できるんだよ
さて・・・
ここで問題がある
大問題だ!
0~1 の数字の受け渡しで、どうして学習できるんだ?
実際、どうやってんだよ!!
というお話だ・・・
中学生にどうやって、教えるんだよ!
という問題
シグモイド関数とか、誤差逆伝播法、 偏微分 とか
悪魔の呪いのような文言、数式を用いずに、どうやってお伝えするかだ・・・
では次回、学習の概念について
たぶん書くと、思うぞ
興味がなくなって書かなかったらす饅頭